Μια τιμή μιας αριθμητικής ποσότητας μπορεί να γραφεί σαν ένας αριθμός σε ένα αριθμητικό σύστημα ορισμένο σε συγκεκριμένη βάση. Έτσι έχουμε τα ακόλουθα αριθμητικά συστήματα:

α) Το δυαδικό σύστημα με βάση το δύο
β) Το δεκαδικό σύστημα με βάση το δέκα
α) Το δεκαεξαδικό σύστημα με βάση το δεκαέξι.

Κάθε αριθμητικό σύστημα χρησιμοποιεί τόσα ψηφία όσα και η βάση του. Έτσι
α) το δυαδικό σύστημα χρησιμοποιεί δυο ψηφία τα 0 και 1
β) το δεκαδικό σύστημα χρησιμοποιεί δέκα ψηφία από 0 έως 9
γ) το δεκαεξαδικό σύστημα χρησιμοποιεί δεκαέξι ψηφία από 0 έως 9 και Α έως F

Ένας ακέραιος αριθμός γραμμένος σε ένα αριθμητικό σύστημα με βάση το r, μπορεί να γραφεί με μια ακολουθία ψηφίων και συγκεκριμένα μπορεί να αποτελείται από ψηφία από το σύνολο των 0, 1, 2, . . . ,r-1. Έτσι ένας αριθμός γραμμένος σε ένα αριθμητικό σύστημα με βάση το r μπορεί να εκφραστεί ως εξής:

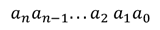
Όπου ο συντελεστής α_j μπορεί να είναι οποιοδήποτε από τα ψηφία: 0, 1, 2, . . .,r-1 . Γενικά, ένας αριθμός γράφεται σε μαθηματική μορφή, σε ένα αριθμητικό σύστημα με βάση το r, σαν άθροισμα με συντελεστές που πολλαπλασιάζονται με δυνάμεις του r, ως εξής:

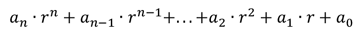
Οι συντελεστές α_j μπορούν να πάρουν οποιαδήποτε τιμή από 0 έως r-1 . Είπαμε ότι, ένας αριθμός γραμμένος σε ένα αριθμητικό σύστημα αποτελείται από μια ακολουθία ψηφίων. Για ένα οποιοδήποτε αριθμό ορίζεται σε κάθε θέση του ψηφίου, η αξία θέσης του. Έτσι ένας αριθμός σε ένα αριθμητικό σύστημα, εκφράζεται σαν το άθροισμα όλων των γινομένων των ψηφίων με την αντίστοιχη αξία θέσης του.

Αξία θέσης

Για ένα δεκαδικό αριθμό, η αξία θέσης από δεξιά προς αριστερά, είναι οι μονάδες, οι δεκάδες, οι εκατοντάδες, οι χιλιάδες κ.τ.λ. Έτσι καθώς μετακινούμαστε μια θέση αριστερά, η αξία θέσης πολλαπλασιάζεται επί 10. Έτσι, π.χ. ο δεκαδικός αριθμός (852)₁₀ εκφράζεται ως δυο μονάδες, πέντε δεκάδες και οκτώ εκατοντάδες.

Για ένα δυαδικό αριθμό, η αξία θέσης από δεξιά προς αριστερά είναι οι μονάδες, οι 2άδες, οι 4άδες, οι 8άδες, οι 16άδες, οι 32άδες, οι 64άδες, οι 128άδες, οι 256άδες κ.τ.λ. Έτσι καθώς μετακινούμαστε μια θέση αριστερά, η αξία θέσης πολλαπλασιάζεται επί 2. Έτσι π.χ. ο δυαδικός αριθμός (1101101)₂ εκφράζεται ως μια μονάδα, μηδέν 2άδες, μια 4άδα, μια 8άδα μηδέν 16άδες, μια 32άδα και μια 64άδα.

Για ένα δεκαεξαδικό αριθμό, η αξία θέσης από δεξιά προς αριστερά είναι οι μονάδες, οι 16άδες, οι 256άδες, οι 4096άδες κ.τ.λ. Καθώς μετακινούμαστε μια θέση προς τα αριστερά, η αξία θέσης πολλαπλασιάζεται επί 16. Έτσι π.χ. ο δεκαεξαδικός αριθμός (2AD)₁₆ εκφράζεται ως δεκατρείς (D) μονάδες δέκα (Α) 16άδες και δυο 256άδες.

Μετατροπή δυαδικού σε δεκαδικό

Η αξία θέσης σε κάθε θέση ψηφίου, στο δυαδικό σύστημα, δίνεται στον ακόλουθο πίνακα:

Σε αυτή την παράγραφο θα δούμε πως μπορούμε να μετατρέπουμε ένα δυαδικό σε δεκαδικό. Για παράδειγμα, δίνεται ο δυαδικός αριθμός 110011. Με τι ισούται στο δεκαδικό; Παρακάτω βλέπουμε τον τρόπο μετατροπής.

Αρχίζουμε από δεξιά και προχωράμε προς τα αριστερά. Για κάθε δυαδικό 1, δίνουμε την δυαδική αξία της θέσης του και το σημειώνουμε κάτω από το δυαδικό ψηφίο. Για να βρούμε το δεκαδικό αντίστοιχο προσθέτουμε τους τέσσερις δεκαδικούς αριθμούς όπως φαίνεται στο σχήμα. Βρίσκουμε ότι, ο δυαδικός αριθμός 110011 αντιστοιχεί στον δεκαδικό 51.

Ένα άλλο πρόβλημα είναι να μετατρέψουμε σε δεκαδικό αριθμό τον δυαδικό 101010. Γράφουμε τον αριθμό με τον ίδιο τρόπο.

Αρχίζοντας από τα δεξιά γράφουμε την αξία θέσης κάθε δυαδικού ψηφίου 1, κάτω από αυτό σε δεκαδική μορφή. Προκύπτουν τρεις δεκαδικοί που τους προσθέτουμε. Έτσι βρίσκουμε ότι ο δυαδικός αριθμός 101010 αντιστοιχεί στο δεκαδικό 42.

Τώρα ας δοκιμάσουμε ένα μεγάλο και δύσκολο δυαδικό αριθμό, τον αριθμό 1111101000. Γράφουμε τον δυαδικό ως εξής:

Εργαζόμαστε ως εξής: μετατρέπουμε κάθε δυαδικό ψηφίο 1 στη σωστή δεκαδική του αξία. Προσθέτουμε και παίρνουμε το συνολικό δεκαδικό αριθμό (1000)₁₀ που αντιστοιχεί στο δυαδικό (1111101000)₂

Μετατροπή δεκαδικού σε δυαδικό

Πολλές φορές ενώ δουλεύουμε με ψηφιακά ηλεκτρονικά, πρέπει να είμαστε σε θέση να μετατρέψουμε ένα δεκαδικό αριθμό σε δυαδικό. Θα μάθουμε μια μέθοδο που θα μας βοηθήσει να κάνουμε αυτή τη μετατροπή.

Έστω ότι θέλουμε να μετατρέψουμε το δεκαδικό αριθμό 13 σε δυαδικό. Μια διαδικασία, που μπορούμε να ακολουθήσουμε, είναι η εξής:

Παρατηρούμε ότι το 13 διαιρείται με το 2 δίνοντας πηλίκο 6 και υπόλοιπο1. Το υπόλοιπο αυτό πάει στη θέση των μονάδων του δυαδικού αριθμού. Στη συνέχεια το 6 διαιρείται με το 2 δίνοντας πηλίκο 3 και υπόλοιπο 0. Το υπόλοιπο 0 πάει στη θέση των δυάδων του δυαδικού αριθμού. Όμοια το 3 διαιρείται με το 2 δίνοντας πηλίκο 1 και υπόλοιπο1 που πάει στη θέση των τετράδων ενώ το πηλίκο 1 διαιρείται με το 2 δίνοντας πηλίκο 0 και υπόλοιπο 1 το οποίο πάει στη θέση των οκτάδων. Έτσι ο δεκαδικός αριθμός 13 μετατράπηκε στον δυαδικό αριθμό 1101.

Ο δεκαδικός αριθμός 37 με τον ίδιο τρόπο γίνεται:

Παρατηρούμε ότι σταματάμε τις διαιρέσεις με το 2 όταν πάρουμε πηλίκο 0. Σύμφωνα με αυτή τη διαδικασία ο δεκαδικός αριθμός 37 αντιστοιχεί στον δυαδικό αριθμό 100101

Δεκαεξαδικοί αριθμοί

Το δεκαεξαδικό σύστημα αριθμών ονομάζεται και «σύστημα με βάση 16» και χρησιμοποιεί 16 σύμβολα, τα οποία είναι 1, 2, 3, 4, 5, 6, 7, 8, 9, Α, Β, C, D, E και F. Ο παρακάτω πίνακας δίνει τις αντιστοιχίες δυαδικών, δεκαδικών και δεκαεξαδικών αριθμών. Παρατηρούμε ότι, το «Α» αντιστοιχεί στο δεκαδικό με το 10, το «Β» με το 11 κ.ο.κ. Το πλεονέκτημα του δεκαεξαδικού συστήματος είναι η χρησιμότητα του στην απευθείας μετατροπή ενός τετραψήφιου δυαδικού αριθμού σε δεκαεξαδικό. Για παράδειγμα, το δεκαεξαδικό F αντιστοιχεί στον τετραψήφιο δυαδικό αριθμό 1111. Οι δεκαεξαδικοί αριθμοί χρησιμοποιούνται για να αντιπροσωπεύσουν ένα δυαδικό αριθμό. Για παράδειγμα ο δεκαεξαδικός αριθμός Α6 αντιπροσωπεύει τον οκταψήφιο δυαδικό αριθμό 10100110. Οι δεκαεξαδικοί αριθμοί χρησιμοποιούνται πολύ στα συστήματα που βασίζονται σε μικροεπεξεργαστές για να αντιπροσωπεύσουν δυαδικούς αριθμούς με 8, 16 ή 32 ψηφία.

Έστω ότι μας ρωτούν πόσα αντικείμενα δηλώνει ο αριθμός 10. Από τον προηγούμενο πίνακα φαίνεται ότι ο αριθμός 10 μπορεί να δηλώνει δέκα, δυο ή δεκαέξι αντικείμενα ανάλογα με τη βάση του αριθμού. Έτσι μερικές φορές σ’ έναν αριθμό προστίθεται και ένας δείκτης για να δηλώσει τη βάση του αριθμού. Χρησιμοποιώντας λοιπόν δείκτες, ο αριθμός 10₁₀ δηλώνει δέκα αντικείμενα. Ο δείκτης (10 στο παράδειγμα μας) δείχνει ότι η βάση του αριθμού είναι το 10 ή ότι ο αριθμός είναι δεκαδικός. Ο αριθμός 10₂ δηλώνει δυο αντικείμενα, γιατί ο αριθμός είναι δυαδικός. Επίσης, ο αριθμός 10₁₆ δηλώνει δεκαέξι αντικείμενα γιατί ο αριθμός είναι δεκαεξαδικός.

Μετατροπή δεκαεξαδικού σε δυαδικό

Η μετατροπή δεκαεξαδικών αριθμών σε δυαδικούς και αντίστροφα, είναι αναγκαία όταν εργαζόμαστε σε μικροεπεξεργαστές και μικροϋπολογιστές. Ας μετατρέψουμε τον C3₁₆ στον αντίστοιχο δυαδικό. Στο ακόλουθο σχήμα κάθε δεκαεξαδικό ψηφίο μετατρέπεται στο αντίστοιχο τετραψήφιο του δυαδικό.

Ο δεκαεξαδικός C αντιστοιχεί στον τετραψήφιο δυαδικό αριθμό 1100 ενώ ο 3₁₆ αντιστοιχεί στον 0011. Ενώνοντας τους δυο δυαδικούς προκύπτει C3₁₆ = 11000011₂

Μετατροπή δυαδικού σε δεκαεξαδικό

Τώρα ας αντιστρέψουμε τη διαδικασία και ας μετατρέψουμε στο δεκαεξαδικό το δυαδικό αριθμό 11101010. Η διαδικασία φαίνεται στο ακόλουθο σχήμα.

Ο δυαδικός αριθμός χωρίζεται σε τετραψήφια γκρουπ, αρχίζοντας από τα δεξιά. Έπειτα, κάθε γκρουπ μετατρέπεται στον αντίστοιχο δεκαεξαδικό αριθμό με τη βοήθεια του πίνακα. Στο παράδειγμα μας έχουμε 11101010₂ = ΕΑ₁₆

Μετατροπή δεκαεξαδικού σε δεκαδικό

Ας μετατρέψουμε τον 2DB₁₆ στον αντίστοιχο δεκαδικό αριθμό. Οι αξίες θέσεων για τις πρώτες τρεις θέσεις του δεκαεξαδικού αριθμού φαίνονται στην κορυφή του παρακάτω σχήματος, σαν 256άδες, 16άδες και 1νάδες.

Στο σχήμα υπάρχουν έντεκα 1νάδες, δεκατρείς 16άδες που ισούνται με 208 και δυο 256άδες που ισούνται με 512. Προσθέτοντας 11+208+512 έχουμε 731₁₀ , δηλαδή έχουμε 2DB₁₆=731₁₀

Μετατροπή δεκαδικού σε δεκαεξαδικό

Τώρα, ας αντιστρέψουμε τη διαδικασία και ας μετατρέψουμε το δεκαδικό αριθμό 47 στον αντίστοιχο δεκαεξαδικό. Στο παρακάτω σχήμα φαίνεται η διαδικασία της συνεχούς διαίρεσης με το 16.

Ο δεκαδικός 47 διαιρείται πρώτα με το 16, δίνοντας πηλίκο 2 και υπόλοιπο 15. Το υπόλοιπο15 (F στο δεκαεξαδικό) γίνεται το λιγότερο σημαντικό ψηφίο του δεκαεξαδικού αριθμού. Το πηλίκο (2 στο παράδειγμα μας) μετατρέπεται σε διαιρετέο  και διαιρείται με το 16 και δίνει πηλίκο 0 και υπόλοιπο 2. Το 2 γίνεται το επόμενο ψηφίο του δεκαεξαδικού αριθμού. Η διαδικασία ολοκληρώθηκε γιατί το πηλίκο είναι μηδέν. Στο σχήμα φαίνεται η μετατροπή του αριθμού 47₁₀ στον αντίστοιχο αριθμό 2F₁₆